Таким образом, источник тока характеризуется как величиной ЭДС, так и величиной собственного внутреннего сопротивления r – обе эти характеристики свидетельствуют о качестве источника.

Электростатические высоковольтные генераторы (как генератор Ван де Граафа или генератор Уимшурста), к примеру, отличаются огромной ЭДС измеряемой миллионами вольт, при этом их внутреннее сопротивление измеряется сотнями мегаом, потому они и непригодны для получения больших токов.

Гальванические элементы (такие как батарейка) — напротив — имеют ЭДС порядка 1 вольта, хотя внутреннее сопротивление у них порядка долей или максимум - десятка Ом, и от гальванических элементов поэтому можно получать токи в единицы и десятки ампер.

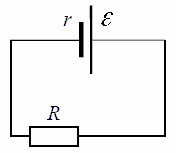На данной схеме показан реальный источник с присоединенной нагрузкой. Здесь обозначены ЭДС источника, его внутреннее сопротивление, а также сопротивление нагрузки. Согласно закону Ома для замкнутой цепи, ток в данной цепи будет равен:

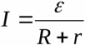Поскольку участок внешней цепи однороден, то из закона Ома можно найти напряжение на нагрузке:

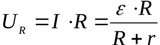Выразив из первого уравнения сопротивление нагрузки, и подставив его значение во второе уравнение, получим зависимость напряжения на нагрузке от тока в замкнутой цепи:

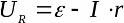В замкнутом контуре ЭДС равна сумме падений напряжений на элементах внешней цепи и на внутреннем сопротивлении самого источника. Зависимость напряжения на нагрузке от тока нагрузки в идеальном случае линейна.

График это показывает, но экспериментальные данные на реальном резисторе (крестики возле графика) всегда отличаются от идеала:

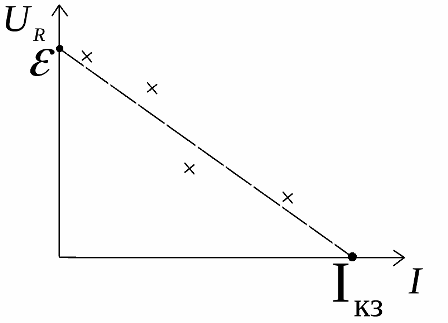Эксперименты и логика показывают, что при нулевом токе нагрузки напряжение на внешней цепи равно ЭДС источника, а при нулевом напряжении на нагрузке ток в цепи равен току короткого замыкания. Это свойство реальных цепей помогает экспериментально находить ЭДС и внутреннее сопротивление реальных источников.

Экспериментальное нахождение внутреннего сопротивления

Чтобы экспериментально определить данные характеристики, строят график зависимости напряжения на нагрузке от величины тока, затем экстраполируют его до пересечения с осями.

В точке пересечения графика с остью напряжения находится значение ЭДС источника, а в точке пересечения с осью тока находится величина тока короткого замыкания. В итоге внутреннее сопротивление находится по формуле:

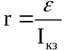Развиваемая источником полезная мощность выделяется на нагрузке. График зависимости этой мощности от сопротивления нагрузки приведен на рисунке. Эта кривая начинается от пересечения осей координат в нулевой точке, затем возрастает до максимального значения мощности, после чего спадает до нуля при сопротивлении нагрузки равном бесконечности.

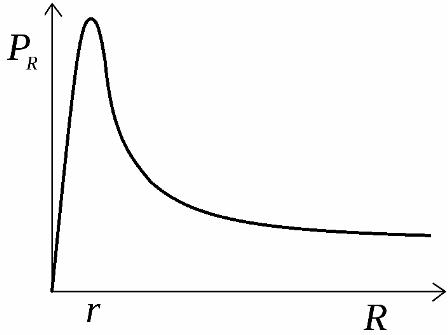Чтобы найти максимальное сопротивление нагрузки, при котором теоретически разовьется максимальная мощность при данном источнике, берется производная от формулы мощности по R и приравнивается к нулю. Максимальная мощность разовьется при сопротивлении внешней цепи, равном внутреннему сопротивлению источника:

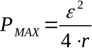Это положение о максимальной мощности при R = r, позволяет экспериментально найти внутреннее сопротивление источника, построив зависимость мощности, выделяемой на нагрузке, от величины сопротивления нагрузки. Найдя реальное, а не теоретическое, сопротивление нагрузки, обеспечивающее максимальную мощность, определяют реальное внутреннее сопротивление источника питания.

КПД источника тока показывает отношение максимальной выделяемой на нагрузке мощности к полной мощности, которую в данный момент развивает источник:

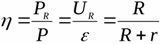Ясно, что если источник развивает такую мощность, что на нагрузке получается максимум возможной мощности для данного источника, то КПД источника окажется равным 50%.