Колебательный процесс в электротехнике и электронике, виды колебаний
23.11.2017 13:47

Колебательный процесс — процесс, обладающий той или иной степенью повторяемости. Все колебательные процессы разделяются на 2 класса: периодические и непериодические. В теории пользуются еще промежуточные классом — почти периодические колебания.

Периодическим называется такой колебательный процесс, при котором характеризующая этот процесс величина, взятая в любой момент времени, через определенный отрезок времени Т имеет то же самое значение.

Функция f(t), являющаяся математическим выражением колебательного процесса, называется периодической с периодом Т, если она удовлетворяет условию f(t+T)=f(t).

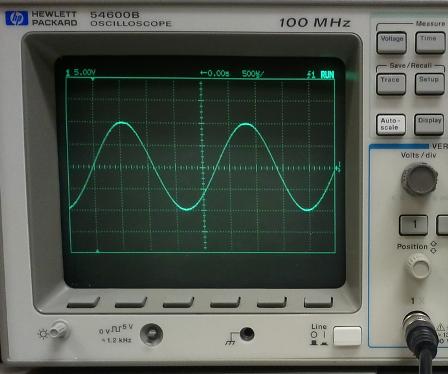Синусоидальные колебания

Среди класса периодических колебательных процессов главную роль играют гармония, или синусоидальные колебания, при которых изменение физической величины со временем происходит по закону синуса или косинуса. Их общая запись имеет вид:

y = f(t) = a·cos·((2π/T)·t - φ),

где a - амплитуда колебаний, φ - фаза колебаний, 1/T = f - частота, а 2πf = ω - циклическая, или круговая частота колебаний.

Применение синусоидальных колебаний и их характеристики:

Переменный ток

Основные параметры переменного тока

Графические способы изображения переменного тока

Почти периодическая функция, соответствующая прочти периодическим колебаниям определяется условием:

|f·(t+τ) - f(t)| , где ε - заданная величина при любом значении t.

Величина τ этом случае называется почти периодом. Если величина ε очень мала по сравнению со средним значением f(t) за время t, то почти периодическая функция будет близка к периодической.

Непериодические колебания гораздо разнообразнее периодических. Но чаще всего в автоматике приходится встречаться с затухающими или нарастающими синусоидальными колебаниями.

Колебания по закону затухающей синусоиды или, как их иногда называют, затухающие гармонические колебания можно представить в общем виде:

х = Ae-δtсos·(ω + φ),

где t — время, А и φ — произвольные постоянные. Общая запись закона нарастающих гармонических колебаний отличается только знаком у коэффициента затухания δ[1/сек].

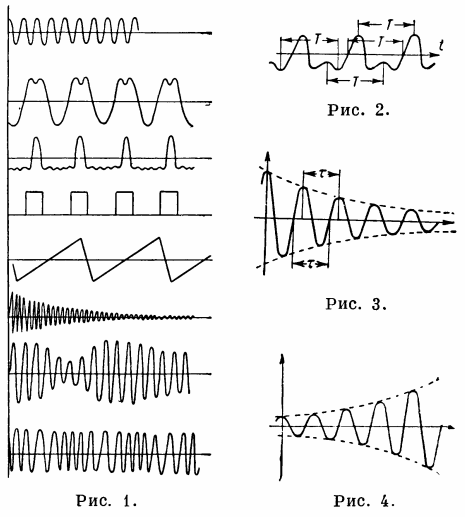Колебательный процесс

Рис.1 - колебательный процесс, рис. 2. - периодический процесс, рис. 3. - затухающие гармонические колебания, рис. 4. - нарастающие гармонические колебания.

Пример применения колебательного процесса — простейший колебательный контур.

Колебательный контур (электрический контур) — пассивная электрическая цепь, в которой могут происходить электрические колебания с частотой, определяемой параметрами самого контура.

Простейший колебательный контур состоит из емкости С и индуктивности L. При отсутствии внешнего воздействия в контуре могут происходить затухающие колебания с частотой fо = 1/2π√LC.

Амплитуда колебаний уменьшается, как e-δt, где δ —коэффициент затухания. Если δ >= fо, то затухающие колебания в контуре становятся не периодическими.

В радиоэлектронике качество колебательного контура определяется добротностью: Q=nf/δ. При воздействии на колебательный контур внешней периодической силы в нем возникают вынужденные колебания. Амплитуда вынужденных колебаний значительно возрастает у высокодобротных контуров, если частота внешнего воздействия близка к fo (резонанс). Колебательный контур является одной из главных частей в резонансных усилителях, генераторах и других электронных приборах.

Смотрите также по этой теме: Применение резонанса напряжений и резонанса токов

Read Full Article